« Je suis fractale » : voilà une de mes expressions favorites du temps où j’étais étudiant à l’IUT informatique de Bordeaux (coucou les amis). Il faut dire qu’à l’époque même boire café sur café ne suffisait pas pour me tenir éveillé tellement mes nuits étaient courtes – je me souviens même que j’ai failli tomber dans les pommes pendant une soutenance à cause d’un café corsé « façon Michael Pujos »* sensé nous sortir de la torpeur d’une nuit blanche. Passons.
Les fractales sont des objets mathématiques qui me plaisent profondément, à la fois par la simplicité du calcul qui permet de les obtenir tout autant que par leur forme parfaite, à la fois si éloignée et proche de la réalité. La plus connue d’entre toutes est certainement l’ensemble de Mandelbrot. Elle s’obtient par un algorithme très simple, d’ailleurs la première fois que j’en ai vu une c’était un programme en basic pour Amstrad CPC qui l’avait générée. Le programme faisait 8 lignes, mais il fallait une journée de calcul pour obtenir l’image…

Un ensemble de Mandelbrot joli.
|
Calcul de l’ensemble de Mandelbrot en GFA basic (320×200 en 16 couleurs) par Fred,
vraiment utile que si vous avez un Atari ST ou un Amiga.
Ce qui est étonnant avec cet ensemble, c’est qu’il n’est obtenu que par l’addition successives de valeurs au carré. Autrement dit, on part de quelque chose qui est sensé être suréloigné de la nature (des additions et des multiplications) et on arrive à un truc qui ressemble à tout sauf à une forme géométrique. Bon, pour être exact on additionne des nombres complexes au carré (vous savez, ai+b… oui enfin vous savez peut-être pas) plutôt que des réels, mais c’est du détail.
Le type qui a pondu cet ensemble fractal est über connu, c’est bien évidemment le vieux Benoît Mandelbrot. C’est d’ailleurs lui qui a le premier repris tous les objets fractals déjà connus par les mathématiciens (ceux-ci, pas fous, évitaient soigneusement de les étudier) et qui en a sorti une théorie et un bouquin qui fait le parallèle entre ce domaine des mathématiques et la nature : Les objets fractals : forme, hasard, et dimension, qu’il faudra décidément que je me choppe un jour.

Un Mandelbrot moche.
Ce cher monsieur travaillant pour IBM a fait pour la première fois le parallèle entre ces objets, qualifiés de « monstrueux » par les mathématiciens de l’époque, et la nature : on retient souvent le fameux exemple de la côte bretonne vue du ciel dont la longueur augmente au fur et à mesure qu’on s’en approche (puisqu’elle est de plus en plus brisée). L’exemple le plus frappant dans la nature restant à mon sens la fougère, mais en fait on retrouve des structures fractales un peu partout. Tout ceci nous amène donc à deux conclusions évidentes : d’une part il y avait bien quelqu’un d’intelligent chez IBM, et d’autre part la côte bretonne ne sert vraiment à rien.

Un chou fractal (chou romanesco).
Vous pouvez vous aussi vous amuser à dessiner des fractales, c’est relativement simple (il faut juste un peu de patience). L’objet le plus connu (et qui date d’avant Mandelbrot) est le flocon de Koch, qui s’obtient de la manière suivante : dessinez un triangle equilatéral (qui a les trois côtés de même longueur). Divisez chaque côté par trois et dessinez un nouveau triangle isocèle sur le segment du milieu, vers l’exterieur. Puis recommencez sur chaque nouveau segment de l’objet obtenu (on appelle ça faire une itération). Si vous réussisez à le faire vingt fois de suite sur une feuille A4, alors vous verrez un Vorlon.

Résultat après un nombre infini d’itérations :

Le flocon de Koch est comme tous les ensembles fractals, un truc joli mais mathématiquement incompréhensible pour le commun des mortels. En effet si on calcule son périmètre après un nombre infini d’itérations, on trouve qu’il est infini. Ça, ça semble encore normal, mais ce qui est tordu c’est que dans le même temps sa surface est égale à 8/5ème de la surface du triangle d’origine, ce qui veut dire qu’un périmètre infini contient une surface finie. Mais pour en arriver là, encore une fois, il vous fera de la patience, beaucoup de patience. D’ailleurs, j’ai pu découvrir un parallèle intéressant avec certains de mes cours de l’IUT puisqu’une durée de cours limitée contenait une quantité d’ennui infinie.
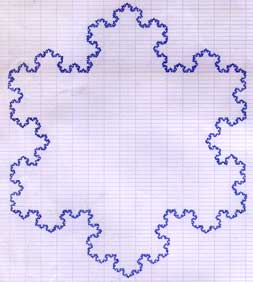
Homemade fractal real amateur XXX hot
Bon, j’avoue, j’ai fait tout ça pour poster ce scan. M’enfin quoi ça a de la gueule quoi merde ! Et pis si vous en voulez des plus jolies pour faire des fonds d’écrans, il y a des galeries sur le net comme celle-ci. Mandelbrot pawa !
* On se souvient du meilleur rôle de Michael Pujos dans le court métrage Salut, c’est moi (page « Profile »)
Les commentaires sont fermés.